Heutzutage ist das kein Problem mehr: GPS-Satellitennavigation für Jedermann macht's möglich. Selbst mit einfachen und erschwinglichen Handempfängern für den Freizeitgebrauch (Abb. 1) lässt sich bereits eine Messgenauigkeit von 3 bis 10 m erzielen. Es ist jedoch Vorsicht geboten: Aus der Vielzahl von Koordinatensystemen, die weltweit verwendet werden, gilt es das richtige auszuwählen. Ansonsten ist die Überraschung groß, wenn der Vergleich mit einer Karte eine Abweichung von mehreren hundert Metern zeigt oder wenn ein Mondberg den Zielstern nicht wie erhofft bedeckt. Dieser Beitrag soll eine kleine Einführung in die Grundlagen der Geodäsie und der Kartografie geben, soweit sie für Amateurastronomen in der Praxis von Bedeutung sind.
Das Prinzip der satellitengestützten Navigation mit dem Global
Positioning System (GPS) ist schnell erklärt. Zur Zeit umkreisen
29 funktionsfähige GPS-Satelliten die Erde. Sie haben genauestens
überwachte Atomuhren an Bord und ihre Bahnen sind mit sehr hoher
Genauigkeit bekannt. Jeder Satellit sendet laufend Signale aus, in
denen die genaue Zeit und die momentane Bahn kodiert sind. Je nach
Entfernung des Empfängers zu den Satelliten treffen diese Signale
unterschiedlich verzögert beim Empfänger ein. Der
Empfänger berechnet aus der Laufzeit der Signale von mindestens
vier Satelliten seine räumlichen Koordinaten und die
Systemzeit. Das Ergebnis wird in der Regel besser, wenn die Signale
von mehr als vier Satelliten in die Auswertung
einfließen. Wichtig ist, dass die benutzten Satelliten
einigermaßen gleichmäßig am vom Empfänger
"sichtbaren" Himmel verteilt sind. Die meisten Empfänger zeigen
die oft zu optimistisch geschätzte Genauigkeit der Messung an
(EPE, "estimated position error" oder ähnlich).
Ein aussagekräftiges Maß für die erzielte Genauigkeit sind die Werte HDOP (horizontal dilution of precision) für die horizontale Position und VDOP (vertical dilution of precision) für die vertikale Position. HDOP und VDOP drücken in Zahlen aus, wie günstig die momentane geometrische Verteilung der Satelliten am Himmel des Beobachters für die Ermittlung der horizontalen und der vertikalen Position ist. Dabei gilt: je kleiner HDOP und VDOP, desto besser die Messung. In der Praxis ist für gute Positionsmessungen HDOP und VDOP<2 anzustreben. Für die geschätzten horizontalen und vertikalen Positionsfehler EPE (95%) in Metern für 95% aller Messungen über einen längeren Zeitraum gilt dann:
Typische Zahlenwerte für den Faktor liegen je nach Ausrüstung zwischen 3 und 6, in ihm stecken die Fehlerquellen für eine GPS-Messung (ionosphärische Störungen, Uhrenfehler im Satelliten, Antennendesign, Empfängerrauschen etc.). Leider zeigen die meisten GPS-Empfänger HDOP und VDOP nicht direkt an; sie müssen dem Gerät über den NMEA-Datenstrom entlockt werden (NMEA=National Marine Electronics Association; standardisiertes Protokoll für den Datenaustausch zwischen elektronischen Geräten in der Nautik; http://www.nmea.org). Dazu wird der GPS-Empfänger mit einem Computer verbunden, auf dem ein Programm läuft, das den NMEA-Datenstrom verarbeiten kann (z.B. SA-Watch [1], VisualGPS [2]).
Der GPS-Betreiber gibt eine horizontale Positionsgenauigkeit von besser als 13 m und eine vertikale Positionsgenauigkeit von besser als 22 m für eine Einzelmessung über 95% einer längeren Messperiode an. In der Praxis lassen sich etwa um einen Faktor zwei bessere Resultate erzielen, wenn mehrere, über einen Zeitraum von Stunden oder Tagen verteilte Messungen gemittelt werden. Am besten achtet man auch darauf, dass der Empfänger vor jeder Messkampagne etwa 20 Minuten ununterbrochenen Satellitenempfang hatte, damit die Almanach-Daten mit Informationen zum Status der Satelliten wirklich aktuell sind.
Es gibt eine Reihe von störenden Einflüssen, die eine GPS-Messung verfälschen können. Der wichtigste Störenfried ist die Erdatmosphäre. Je nach Zustand der Ionosphäre wird die Signallaufzeit verändert und damit das Resultat verfälscht. Diese Störungen werden normalerweise bei einfachen GPS-Empfängern, die nur auf einer Frequenz arbeiten, in grober Näherung korrigiert. In "unruhigen" Zeiten mit starker Sonnenaktivität ist dieses Fehlermodell nicht ausreichend; es kann zu größeren atmosphärisch bedingten Fehlern in der GPS-Position kommen. Im Allgemeinen gilt, dass die atmosphärischen Störungen nachts etwas kleiner sind als tagsüber.
Der Einfluss atmosphärischer Störungen auf die GPS-Messung lässt sich durch den Empfang von zusätzlichen Korrektursignalen deutlich verringern. Feste Bodenstationen ermitteln dauernd regional gültige Korrekturen, die als terrestrisches Radiosignal (differentielles GPS, DGPS) oder über einen geostationären Satelliten zu empfangen sind (WAAS in Nordamerika [3], EGNOS in Europa [4]). Neuere GPS-Empfänger sind in der Regel WAAS- und EGNOS-tauglich. Die Genauigkeit einer GPS-Einzelmessung liegt mit dieser Ergänzung für 95% der Zeit bei besser als 3 m in der Horizontalen und besser als 6 m in der Vertikalen.
Bei der Auswertung der Satellitensignale wird vom Empfänger auch die GPS-Systemzeit und UTC mit sehr großer Genauigkeit ermittelt. Bei den meisten GPS-Handempfängern hat die Anzeige der Zeit aber nur eine niedrige Priorität. Verzögerungen von 1 bis 2 Sekunden sind üblich. Das ist für einige Anwendungen wie die Beobachtung von Sternbedeckungen leider deutlich zu schlecht.
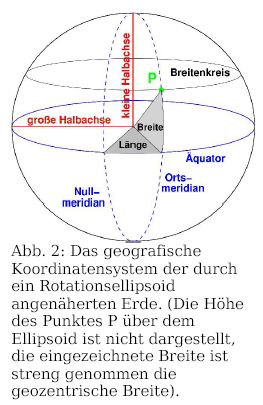Die Erde ist durch ihre Rotation ein wenig abgeplattet. Die Form des
Erdkörpers lässt sich in guter Näherung als
Rotationsellipsoid mit den Parametern große (äquatoriale)
und kleine (polare) Halbachse bzw. große (äquatoriale)
Halbachse und Abplattung beschreiben. Die Lage eines Punktes P auf der
Erde ist dann durch die Angabe seiner Abweichung von der
Ellipsoidoberfläche ("Höhe" über dem Ellipsoid) sowie
seiner Winkelkoordinaten Länge (relativ zu einem Nullmeridian)
und Breite (relativ zum durch die Rotation definierten Äquator)
eindeutig bestimmt (Abb. 2).
In der Vermessungskunde wird der Begriff des Geoids zur Beschreibung des Erdkörpers verwendet. Das Geoid ist der Körper, an dessen Oberfläche das einheitliche Schwerkraftniveau der mittleren Meeresoberfläche der Erde herrscht ("Äquipotentialfläche"). Es zeigt sich, dass das Geoid gegenüber einem Rotationsellipsoid Dellen und Ausbuchtungen von der Größenordnung bis 100 m hat. Doch davon wussten die großen Geodäten der Geschichte wie Gauß oder Bessel, auf deren Arbeiten die deutsche Landvermessung auch heute noch gründet, noch nichts.
Historisch versuchte man, aus astronomischen und anderen Messungen die optimalen Parameter des Rotationsellipsoids herauszufinden, das die Erde beschreiben sollte. Auf diese Weise entstanden "lokale" Anpassungen für die jeweiligen Länder, die jedoch den Erdkörper insgesamt nicht optimal charakterisieren. So wird z.B. für die Kartografie in Deutschland, Österreich und der Schweiz auch heute noch das Ellipsoid nach Bessel 1841 verwendet (siehe Tabelle 1).
Die umfassende und konsistente Vermessung des Erdkörpers ist erst mit der Satellitentechnologie der letzten Jahrzehnte möglich geworden. Das derzeit für globale Zwecke am häufigsten benutzte Ellipsoid wurde WGS84 (World Geodetic System 1984) genannt. Die national gebräuchlichen Ellipsoide können sich vom WGS84-System in folgenden Parametern unterscheiden: große Halbache, Abplattung, Differenz der Mittelpunktskoordinaten, Verkippung der Achsen gegeneinander, Maßstab. Entsprechend können sich die Koordinaten ein und desselben Punktes auf der Erdoberfläche je nach Bezugsellipsoid und relativer Orientierung der Ellipsoide voneinander unterscheiden.
Die Parameter, die ein geodätisches Bezugssystem vollständig charakterisieren, werden als Datums-Parameter bezeichnet. In der deutschen Geodäsie/Kartografie wird heute üblicherweise das historisch gewachsene Potsdam-Datum mit Zentralpunkt Rauenberg verwendet, in Österreich ist das Datum MGI mit Zentralpunkt Hermannskogel gebräuchlich. In der Schweiz ist zur Zeit meist noch das Datum CH1903 in Gebrauch (Tabelle 2).
Wer eine Landkarte herstellen möchte, hat ein
grundsätzliches Problem: Die Oberfläche einer Kugel oder
eines Ellipsoids lässt sich nicht auf eine Ebene abwickeln wie
etwa die Oberfläche eines Würfels. Bei der Darstellung
("Projektion") der Erdoberfläche auf einem ebenen Blatt treten
daher immer Verzerrungen auf. Man kann aber durch geschickte Wahl der
Projektion (mathematisch: Abbildung) erreichen, dass Längen,
Winkel oder Flächen erhalten bleiben.
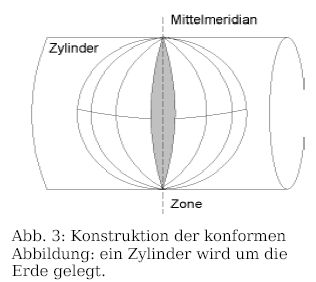
In der deutschen Kartografie wird eine von C.-F. Gauß und L. Krüger entwickelte winkeltreue (konforme) Abbildung verwendet. Man wählt einen Bezugsmeridian auf dem Besselschen Erdellipsoid, legt einen Zylinder mit entsprechendem elliptischem Querschnitt um das Ellipsoid mit Berührungsline Bezugsmeridian herum und projiziert alle Punkte des Ellipsoids in einem Bereich beiderseits des Bezugsmeridians auf die Zylinderfläche (Abb. 3). Die Zylinderfläche lässt sich dann auf eine Ebene abwickeln ("Karte"). Auf der Zylinderfläche/Ebene wählt man ein rechtwinkliges Koordinatensystem, die sogenannten Gauß-Krüger-Koordinaten oder transversalen Mercator-Koordinaten; Nullpunkt der nach Osten positiv gezählten Abszisse ("Rechtswert") ist der Bezugsmeridian, dem der Wert +500000 m zugewiesen wird, um negative Zahlen westlich des Bezugmeridians zu vermeiden. Die Ordinate ("Hochwert") gibt den Abstand vom Äquator entlang des Bezugsmeridians in m wieder (Tabelle 3). Die so konstruierten Gauß-Krüger-Koordinatenlinien sind im Gegensatz zu den geografischen Koordinatenlinien Geraden auf der Karte. Auf Karten mit einem Gauß-Krüger-Koordinatennetz lassen sich die Koordinaten eines Ortes also mit wenig Aufwand ablesen (Abb. 5). Gauß-Krüger-Koordinaten in Deutschland beziehen sich immer auf das Potsdam-Datum.
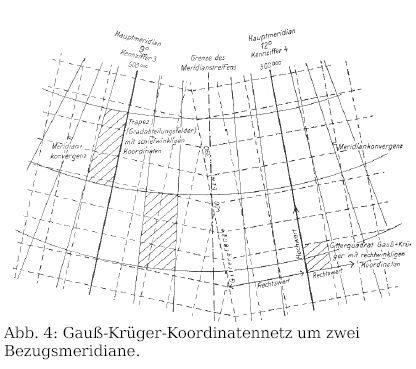Um die Verzerrungen klein zu halten, gibt es in Deutschland die
Bezugsmeridiane 3°, 6°, 9°, 12° und 15° Ost, die von 1 bis 5
durchnummeriert werden. Diese Bezugsmeridiankennzahl wird als erste
Ziffer dem Rechtswert vorangestellt; ein Ort auf 9° östlicher
Länge hat also den Rechtswert 3500000 m (Abb. 4).
Für die Umrechnung von Gauß-Krüger-Koordinaten in die geografischen Koordinaten Länge und Breite gibt es verschiedene mathematische Algorithmen (siehe z.B. [5]). Die so berechneten geografischen Koordinaten beziehen sich auch auf das Potsdam-Datum.
Die meisten GPS-Handempfänger können Gauß-Krüger-Koordinaten für Deutschland direkt anzeigen. Dazu wählt man im entsprechenden Menü das Koordinatensystem "German Grid" oder ähnlich aus. Der GPS-Empfänger sollte von sich aus dazu das Potsdam-Datum aktivieren. Falls "German Grid" oder entsprechendes nicht verfügbar ist, kann man Gauß-Krüger-Koordinaten auch über das benutzerdefinierte Koordinatensystem und Datum bekommen (Parameter siehe Tabellen 3 und 2). Achtung: GPS-Empfänger der Firma Magellan zeigen bei "German Grid" nicht ganz richtige Gauß-Krüger-Koordinaten an. Deshalb aktiviert man Gauß-Krüger-Koordinaten bei Magellan-Geräten am besten über das benutzerdefinierte Koordinatensystem und Datum (Tabellen 3 und 2).
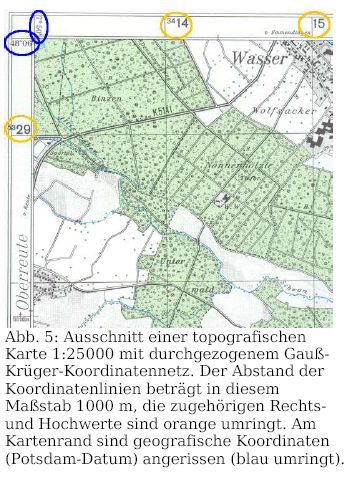Die von den Landesvermessungsämtern herausgegebenen gedruckten
topografischen Karten beziehen sich auf das Potsdam-Datum. Sie sind in
regelmäßigen Längen- und Breitengradintervallen
geschnitten. Das Gauß-Krüger-Koordinatennetz ist teilweise
über das ganze Kartenblatt ausgezogen oder am Rand in
regelmäßigen Abständen angerissen (Abb. 5). Bei den
digitalen topografischen Karten der TOP-Serien, die auch von den
Landesvermessungsämtern herausgegeben werden, kann man das
Koordinatensystem wählen (z.B. geografische, UTM- oder
Gauß-Krüger-Koordinaten, Potsdam oder WGS84-Datum).
In Österreich sind Gauß-Krüger-Koordinaten ähnlich denen in Deutschland gebräuchlich (siehe Tabelle 3). Sie beziehen sich auf das Datum MGI mit Zentralpunkt Hermannskogel. In den dem Autor bekannten GPS-Empfängern müssen die österreichischen Gauß-Krüger-Koordinaten über das benutzerdefinierte Koordinatensystem und Datum aktiviert werden (mit Parametern aus Tabellen 3 und 2). In der Schweizer Landesvermessung wird ein rechtwinkliges Koordinatengitter ("Schweizer Landeskoordinaten") verwendet, das durch eine gekippte transversale Mercator-Projektion entsteht. Fundamentalpunkt ist die alte Sternwarte in Bern (Parameter siehe Tabelle 3). Bei GPS-Empfängern heißen die Landeskoordinaten "Swiss Grid" oder ähnlich. Nähere Informationen sind beim Schweizerischen Bundesamt für Landestopografie erhältlich [6]. Für einige, hauptsächlich europäische Länder hat Stefan Voser entsprendende Informationen im Internet zusammengestellt [7].
GPS-Nutzer können die Ermittlung der geografischen WGS84-Koordinaten einfach dem GPS-Empfänger überlassen. Sie wählen dazu die Optionen "geografische Koordinaten" als Koordinatensystem und "WGS84" als Datum. Die so erhaltenen Koordinaten können aber nicht mehr unmittelbar in eine gedruckte topografische Karte mit nationalem Datum übertragen werden.
Beide Rechenschritte lassen sich mit dem GPS-Empfänger erledigen. Dabei nützt man aus, dass die Koordinaten eines Wegpunkts immer im gerade eingestellten (primären) Koordinatensystem und Datum des GPS-Empfängers ausgegeben werden. Man wählt also zunächst das Koordinatensystem und Datum, in dem die Koordinaten gegeben sind, speichert die Koordinaten als Wegpunkt, wechselt dann im GPS-Empfänger zu geografischen Koordinaten und WGS84-Datum und lässt sich die umgerechneten Koordinaten des Wegpunkts wieder anzeigen.
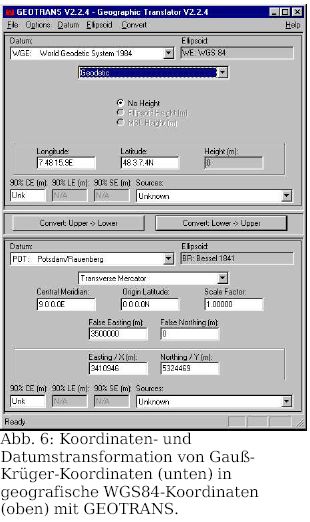Es gibt auch Computerprogramme, die die Umrechnungen
durchführen. Ein sehr nützliches Freeware-Tool ist GEOTRANS,
das im Internet [9] zu beziehen ist. GEOTRANS
kann die Koordinaten- und Datumtransformation in einem Schritt
berechnen. Für Umrechnungen vom oder in das Potsdam-Datum
bzw. vom oder in das CH1903-Datum müssen die entsprechenden
Transformationsparameter zuvor als neues Datum eingegeben werden
(siehe Tabelle 2).
GEOTRANS und die GPS-Empfänger verwenden für die Datum-Transformation ein vereinfachtes mathematisches Modell, die sogenannte Molodensky-Transformation. Verkippungen der beiden Bezugsellipsoide gegeneinander sowie Maßstabsänderungen werden hierbei vernachlässigt. Für eine Genauigkeit im Bereich einige Meter ist das ausreichend; wer genauere Ergebnisse benötigt, muss eine sogenannte Helmert-Transformation durchführen [10].
Abschließend sei noch auf eine Besonderheit bei der Transformation der Höhen hingewiesen, die sich für Amateurastronomen allerdings nur bei besonders hohen Genauigkeitsansprüchen bemerkbar machen wird, etwa bei streifenden Sternbedeckungen durch den Mond. Höhenangaben, die aus einer topografischen Karte abgelesen werden, sind sogenannte orthometrische Höhen. Sie beziehen sich auf einen Höhennullpunkt Normal Null (NN, in etwa Meeresspiegel). Das Nullniveau eines lokal angepassten Ellipsoids wie etwa des Bessel-Ellipsoids in der deutschen Landvermessung weicht für unsere Zwecke vernachlässigbar wenig vom orthometrischen Nullniveau ab. Das globale WGS84-Ellipsoid jedoch liegt im deutschen Sprachraum zwischen 30 und 50 m unter dem Geoid; um die tatsächliche Höhe des Beobachtungsorts über dem WGS84-Ellipsoid zu erhalten, muss zu seiner orthometrischen Höhe noch die Geoid-Höhe an diesem Punkt dazugezählt werden. Die Geoid-Höhe eines Ortes kann z.B. mit GEOTRANS oder auf der Internetseite [11] berechnet werden. Auch die dem Autor bekannten GPS-Handempfänger zeigen orthometrische Höhen an. Intern wird zwar die Höhe über dem WGS84-Ellipsoid berechnet, angezeigt wird aber die mit Hilfe eines einfachen Geoid-Modells korrigierte orthometrische Höhe. Das gilt auch dann, wenn ausdrücklich das WGS84-Datum eingestellt ist. GPS-Nutzer sollten in der Bedienungsanleitung ihres Empfängers nachlesen, ob WGS84-Höhen ausgegeben werden können. Manche Empfänger stellen die verwendete Geoid-Höhe über den NMEA-Datenstrom für entsprechende Computerprogramme wie VisualGPS zur Verfügung.
[2] VisualGPS: Freeware-Programm zur Darstellung und Analyse der NMEA-Daten eines GPS-Empfängers; http://www.visualgps.net/VisualGPS/default.htm
[3] WAAS (Wide Area Augmentation System), siehe z.B. http://www.kowoma.de/gps/waas_egnos.htm
[4] EGNOS: http://www.esa.int/export/esaSA/GGG63950NDC_navigation_0.html
[5] Wepner, W.: Mathematisches Hilfsbuch für Studierende und Freunde der Astronomie, Treugesell-Verlag Dr. Vehrenberg KG, Düsseldorf
[6] Internetseite des Schweizerischen Bundesamtes für Landestopografie: http://www.swisstopo.ch
[7] Internetseite von Stefan Voser mit Informationen zu den Kartengrundlagen einiger Länder: http://www.geocities.com/mapref/mapref.html
[8] Meeus, J.: Astronomical Algorithms, Kapitel 10; Verlag Willmann-Bell, Inc., Richmond (Virginia), 1991
[9] GEOTRANS: Freeware-Programm zur Koordinaten- und Datumstransformation; http://earth-info.nima.mil
[10] http://www.posc.org/Epicentre.2_2/DataModel/ExamplesofUsage/eu_cs35.html
[11] Berechnung von Geoidhöhen relativ zum WGS84-Ellipsoid: http://earth-info.nima.mil/GandG/egm96/intpt.htm
| Parameter | Bessel (1841) | WGS84 |
|---|---|---|
| große Halbachse a | 6377397.155 m | 6378137.0 m |
| kleine Halbachse b | 6356078.963 m | 6356752.3 m |
| reziproke Abplattung 1/f | 299.1528128 | 298.257223563 |
Tabelle 1: einige Parameter für das Bessel (1841)-Ellipsoid und für das WGS84-Ellipsoid.
| Parameter | Potsdam (D) | MGI (A) | CH1903 (CH) |
|---|---|---|---|
| Delta a (große Halbachse) | 739.845 m | ||
| Delta f*10**4 (Abplattung) | 0.10037483 | ||
| Delta X (Offset Mittelpunkt x) | +587 m | +575 m | +674.4 m |
| Delta Y (Offset Mittelpunkt y) | + 16 m | + 93 m | + 15.1 m |
| Delta Z (Offset Mittelpunkt z) | +393 m | +466 m | +405.3 m |
Tabelle 2: Parameter für die genäherte Datumstransformationen Potsdam, MGI, CH1903 nach WGS84 (Molodensky-Transformation). Für eine höhere Genauigkeit als 15 m muss eine Helmert-Transformation verwendet werden, die Verkippungen der Achsen gegeneinander und unterschiedliche Maßstäbe berücksichtigt.
| Parameter | Gauß-Krüger-Koordinaten (D) | Gauß-Krüger-Koordinaten (A) | Schweizer Landeskoordinaten (CH) |
|---|---|---|---|
| Projektion | Transversale Mercator-Projektion | Transversale Mercator-Projektion | Transversale Mercator-Projektion |
| Nullpunkt Breite | 0° | 0° | 46.952406° Nord |
| Nullpunkt Länge | Bezugsmeridian 3°, 6°, 9°, 12°, 15° Ost | 10°20', 13°20', 16°20' Ost | 7.439583° Ost |
| Skalenfaktor | 1.0 | 1.0 | 1.0 |
| False easting am Längennullpunkt | [n]500000 m *) | [m]500000 m **) | 600000 m |
| False northing am Breitennullpunkt | 0 m | 0 m | 200000 m |
| Geodätisches Datum | Potsdam/Rauenberg | MGI/Hermannskogel | CH1903 |
*) n=Nr. des Bezugsmeridians n=1 für 3°Ost, n=2 für 6°Ost usw.
**) m=1 für Bezugsmeridian 10°20' Ost (Zone M28), m=4 für
Bezugsmeridian 13°20' Ost (Zone M31), m=7 für Bezugsmeridian 16°20'
Ost (Zone M34)
Tabelle 3: Parameter für die deutschen und österreichischen Gauß-Krüger-Koordinatensysteme und die Schweizer Landeskoordinaten
Anschrift des Verfassers: Dr. Martin Federspiel, Rosenstr. 1A, 79108 Freiburg-Hochdorf, E-mail: martin"punkt"federspiel"at"gmx"punkt"de